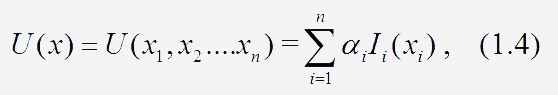Управленческая теория измерений. Часть 2. Шкалы и накладываемые ими ограничения

 

Андрей Мицкевич

Различные измерения и показатели используются в каждой фирме, в любой организации. Выбор подходов к оценке степени достижения некоторого показателя (например, плана продаж) огромен: тут сколько людей, фирм, ситуаций, видов работ, столько и мнений. Задача этой статьи не придумывать что-либо своё, а попытаться классифицировать доминирующее большинство существующих подходов к измерению показателей.
В соответствии с теорией измерений при моделировании реального явления следует прежде всего установить типы шкал, в которых измеряются или должны быть измерены те или иные переменные. Что такое шкала? Какими они бывают? Какие ограничения накладываются на числа, используемые для измерений? Как правильно пользоваться шкалами, чтобы получить достоверные первичные измерения? Какие интегральные и комплексные показатели могут быть построены на множестве измерений, выполненных в различных шкалах?

Шкалы и их классификации

Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.

Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).

Шкалирование — это:

• выбор шкалы для первичных измерений;
• перевод измерения из одной шкалы в другую.

Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.

Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается.
Шкалы, как правило, объединяют в три основные группы:

•  номинальные — для качественных измерений;
•  порядковые — для отражения отношения порядка (больше, лучше, важнее, проще, правильнее и т. п.);
•  количественные — оперируют с числами так, как мы привыкли со школьных времен (например, 10 в 2 раза больше, чем 5).

Иногда все шкалы измерения делят на два класса:

•  шкалы качественных признаков (порядковая шкала и шкала наименований);
•  шкалы количественных признаков (количественные шкалы).

Далее мы последовательно разберём все типы шкал.

Номинальные шкалы

Номинальная шкала (nominal scale), или шкала наименований 1, сопоставляет каждый объект с определённым признаком. В результате объект либо обладает этим признаком, либо нет. Номинальная шкала состоит из названий — это самое простое и в то же время верное понимание номинальной шкалы.
Пример. Красное или чёрное — это измерение в некой цветовой гамме. Многие классификации, ответы на вопросы анкеты — всё это примеры номинальных измерений. С них начинается работа создателей сбалансированной системы показателей, а закончиться она должна цифрами. Но здесь важно не переборщить и оставить номинальные измерения только там, где они предпочтительнее формальной оцифровки.

Как правильно пользоваться шкалами, чтобы получить достоверные первичные измерения? Это не такой простой вопрос, как кажется на первый взгляд.

Допустимые преобразования. В номинальной шкале допустимыми преобразованиями (см. врезку) являются все взаимно-однозначные преобразования 2. Например, red — это «красный». Никаких отношений, кроме «равно» и «неравно», здесь нет. В этой шкале числа используются лишь как метки (как, например, при сдаче белья в прачечную), то есть лишь для различения объектов.

Порядковые шкалы

Порядковая шкала отражает более высокий уровень измерений, учитывающий, к какой категории принадлежит объект и в каком отношении он находится с другими объектами. В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между ними.
Пример. Простейшим примером порядковой шкалы служат оценки знаний учащихся. Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе тот же смысл выражается словесно — «неудовлетворительно», «удовлетворительно», «хорошо», «отлично». Этим подчёркивается «нечисловой» характер оценок знаний студентов.
Фактически измерение по порядковой шкале представляет собой операцию упорядочения. Предполагаются сравнения «больше — меньше» или «лучше — хуже». Например, мнения экспертов часто выражаются в порядковой шкале, то есть эксперт может сказать (и обосновать), что один показатель качества продукции важнее, чем другой; первый технологический объект опаснее, чем второй, и т. д. Но он не в состоянии сказать, во сколько раз или насколько он более важен, или, соответственно, более опасен.
Допустимые преобразования. Порядковая шкала допускает любое возрастающее преобразование, то есть такое, которое не меняет порядок шкалы.
Типы порядковых шкал. Используют два типа порядковых шкал, которые различны с практической точки зрения:

• ранговая шкала, которая предполагает присвоение объектам рангов (ранжирование);
• балльная шкала, в которой применяются баллы.

Обдумывание измерений некоторых показателей следует начать с выбора между ранговым и балльным типами шкал.

Ранговые порядковые шкалы

Ранговые шкалы — это шкалы, где числа служат только для присвоения мест. Экспертов часто просят ранжировать (упорядочить) объекты экспертизы, то есть расположить их в порядке возрастания (или убывания) интенсивности исследуемой характеристики. Ранг — это номер объекта экспертизы в упорядоченном ряду значений характеристики у различных объектов. Формально ранги выражаются числами 1, 2, 3.... Важно помнить, что измерения 1, 2, 3 и 6, 10, 50 означают одно и то же: первая альтернатива заняла первое место, вторая — второе место и т. д. В ранговых шкалах нет информации о величине различий между оцениваемыми объектами. Такие шкалы используются тогда, когда объект трудно описать несколькими характеристиками, которые потом оцениваются качественно (баллами, например) или количественно. В практике менеджмента рейтинги часто основаны на ранговых шкалах.

Ранговые измерения (процедуры ранжирования). Различают несколько основных типов алгоритмов ранжирования:

1. процедура непосредственного ранжирования, когда эксперт должен просто упорядочить объекты. При ранжировании он располагает объекты в порядке предпочтения, руководствуясь знаниями, собственными соображениями и пр. — по сути, расставляет объекты в определённом порядке, пользуясь своим собственным алгоритмом и не объсняя, почему он выбрал именно этот вариант;
2. процедура опосредованного ранжирования, когда эксперт должен упорядочить объекты и дать пояснения;
3. процедура последовательного непосредственного ранжирования, когда эксперт сначала должен отнести объекты к одному из нескольких классов, которым заранее присвоил ранги, а затем упорядочить объекты внутри каждого класса. Метод используется при большом количестве объектов ранжирования;
4. «метод пузырька» взят из программирования, где он применятется для сортировок. Эксперт должен найти место (N+1)-ого объекта в ряду уже упорядоченных N-объектов. Такая процедура весьма экономна и точна;
5. процедура парных сравнений заключается в том, что эксперт устанавливает порядок объектов путём сравнения всех возможных их пар. Это самый точный, но и самый трудоёмкий метод. Перевод результатов таких парных сравнений в ранги не так прост, пример неверного перевода результатов парных сравнений в ранги приведен во врезке.

Корректные методы перевода результатов парных сравнений в шкалу интервалов. Они существуют. Считая предпочтение некоторой случайной величиной, отражающей истинное соотношение характеристик объектов сравнения, можно решить задачу определения вероятности истинного соотношения сравниваемых объектов (модели Брэдли-Терри, Терстоуна-Мостеллера, Льюса и др.). Пример такого корректного перевода дан во врезке. Большого практического значения он не имеет, и чтобы понять его суть, надо хорошо знать математическую статистику 3. Но важно понимать, что такие методы существуют и у них есть обоснование, пусть и небесспорное. В результате метод парных сравнений позволяет определить значимость различий положения тех или иных объектов в иерархии, а также решать другие сходные задачи.

Балльные порядковые шкалы

Балльные шкалы используются очень часто, примеры мы уже приводили. Однако важно понимать, что каждому баллу необходимо присвоить качественную характеристику, в противном случае может пострадать корректность. Приведу пример: в конце 1990-х гг. я был назначен ответственным преподавателем (качество, контроль, апелляции) на устном экзамене по экономике для абитуриентов НИУ ВШЭ. Только что на ректорате ввели 10-балльную шкалу. Экспромт не удался — первый блин, как обычно, вышел комом. Моя работа заключалась, в том числе, и в „обеспечении справедливости”, то есть чтобы за примерно одни и те же ответы преподаватели в разных комиссиях ставили одинаковые баллы. Разброс в оценках оказался ужасающим — от 4 до 7 за похожие ответы. Буквально на следующий день ошибка в дефиниции шкалы была исправлена, а получившаяся шкала (см. таблица 2) успешно работает до сих пор (с небольшим изменением). Многие вузы взяли её на вооружение. Обращаю внимание читателей, что в соответствии со спецификой каждого предмета преподаватель конкретизирует шкалу.

Таблица 2. Пример 10-балльной шкалы для оценки успеваемости студентов.

Балл	Качественная характеристика
10	Пять с плюсом — исключительные знания (кое-что из ответа студента даже преподаватель не знал)
9	Отлично, твёрдая пятёрка
8	Пять с минусом
7	Четыре с плюсом
6	Четыре, твёрдая четвёрка
5	Четыре с минусом
4	Три с плюсом
3	Три, твёрдая оценка «удовлетворительно»
2	Три с минусом
1	Неудовлетворительно

Важный вопрос: какова идеальная размерность балльной шкалы? Ответ: сколько качеств, столько и баллов. Баллы обозначают упорядоченные качества, и каждому качеству присваивают свой балл. Обратное неверно: если взять за основу 10-балльную шкалу и каждому баллу попытаться „присвоить” определённое качество, то можно столкнуться с ситуацией, что качеств может оказаться не 10, а всего 7. Поэтому следует отталкиваться именно от количества качеств, которые вы можете выделить.

Если нет обоснования логики присвоения баллов, будем считать измерение некорректным. Это необходимо для корректного выставления балльных оценок.

Балльные измерения. Балльные измерения формально просты, но коварны возможностью допустить необоснованные оценки и тем самым всё испортить. Существует два подхода к выставлению балльных оценок:

1. непосредственная балльная оценка представляет собой приписывание объектам баллов на основании субъективного представления. Такая оценка используется в социологии, но в управлении компанией применяться не должна (за исключением, пожалуй, начальной стадии разработки системы показателей). Причина проста — слишком произвольно баллы приписываются объектам, трудно объяснить, почему мы по 10-балльной шкале ставим 5, а не 6, например;
2. балльная оценка с обоснованием — это процедура приписывания объектам баллов на основании степени близости к описанным баллами качествам. На мой взгляд, это необходимо для корректного выставления балльных оценок. Примем следующее правило если нет обоснования логики присвоения баллов, будем считать измерение некорректным.

Перевод результатов балльных оценок в весовые коэффициенты. Если такой перевод делается одним экспертом — это операция сомнительная, но популярная. Во врезке приведён один из популярных методов — метод последовательных сравнений.

Перевод рангов в весовые коэффициенты одним экспертом. Метод последовательных сравнений

Продолжим пример, приведённый во врезке. Итак, эксперт проводит оценку четырёх целей, связанных с решением кадровой проблемы. Варианты ранжируются таким образом: Z1, Z3, Z4, Z2.
Шаг 1. Все оцениваемые объекты располагаются в порядке убывания их важности. Назначаются предварительные оценки важности, сумма которых отличается от 100. При этом первый объект массива получает оценку 100, остальные — в соответствии с их важностью. Выставляем предварительные оценки (условные баллы):
p1 = 100, p3 = 60, p4 = 40, p2 = 10.
Шаг 2. Первый объект массива сравнивается со всеми возможными комбинациями нижестоящих объектов, причём в каждой комбинации берётся по два таких объекта. Считается, что комбинацию можно рассматривать как сумму, то есть оба объекта „реализуются”. При необходимости оценка первого объекта корректируется.
Выполним сравнение целей и корректировку их оценок: Z1 сравниваем с (Z3 и Z4) (то есть цель Z1 сравниваем с комбинацией Z3 и Z4), затем Z1 сравниваем с (Z3 и Z2) и так далее. Допустим, эксперт полагает, что Z1 лучше, чем Z3 и Z4 вместе взятые, но Z3+Z4 в сумме составляют 100 условных баллов, поэтому корректируем оценку: p1 = 125.
Шаг 3. Второй объект массива сравнивается со всеми возможными комбинациями нижестоящих объектов, причём в каждой комбинации снова берётся только по два таких объекта. При необходимости корректируется оценка второго объекта и т. д.
Например, Z3 сравниваем с (Z4 и Z2). Остальные сравнения не приносят ничего нового.
Шаг 4. Производятся нормирование скорректированных оценок и расчёт на их основе весов объектов. Запишем скорректированные оценки и вычислим веса целей:
p1 = 125; p3 = 60; p4 = 40; p2 = 10;
v1 = 125/сумма всех оценок = 0,54; v3 = 0,25; v4 = 0,17; v2 = 0,04.
Теперь эти веса можно использовать в аддитивной функции полезности 4.
Корректность вычислений вам предстоит оценить позже, после знакомства с количественными шкалами и оценками, получаемыми на основе измерений в них.

Количественные шкалы

Количественные шкалы отражают более высокий уровень измерений, учитывающий не только то, в каком отношении измеряемый объект находится с другими объектами, но и степень их различия. Примеры использования количественных шкал мы видим повсюду.
Допустимые преобразования. Количественные шкалы определены с точностью до преобразований, которые не меняют единицы измерения (линейных или иных функциональных преобразований).
Типы количественных шкал. Различают количественные шкалы:

• интервалов;
• степеней;
• отношений;
• разностей;
• абсолютную шкалу.

Расположение шкал в этом списке не случайно. Первая (шкала интервалов) — самая слабая по информативности и самая сильная в плане надёжности оценок, последняя (абсолютная шкала) — наиболее информативная (измерения могут быть очень надёжными), но при этом допускающая наименее надёжные оценки. Оценка степени соответствия некоторому идеалу максимально затруднена — помните разницу между оценкой и измерением?
Шкала интервалов (интервальная шкала) точно определяет величину интервала между точками на шкале. Для проведения измерений необходимо задать интервал (2 точки). Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования вида: F(Х) = а · Х + b, где а > 0. 

Шкала степенная. Шкала степеней (степенная) допускает степенное преобразование (F(Х) = АХВ). В области техники она вполне адекватна — у неё тоже две степени свободы, как у шкалы интервалов. В экономике она, напротив, является исключением, поэтому подробно рассматривать её не будем.

Шкала интервалов — самая слабая по информативности и дающая самые надёжные оценоки. Абсолютная шкала — наиболее информативная, но допускающая наименее надёжные оценки. Оценка степени соответствия некоторому идеалу в абсолютной шкале максимально затруднена — помните разницу между оценкой и измерением?

Шкала отношений. Из количественных шкал в науке и практике наиболее распространены шкалы отношений. В них есть естественное начало отсчёта — ноль (то есть отсутствие величины), но нет естественной единицы измерения.
Примеры использования шкалы отношений:

• измерение большинства физических единиц: массы тела, длины, а также цены в экономике;
• любое процентное соотношение — это измерение в шкале отношений;
• простые индексы типа Выручка текущего года/Выручка прошлого года также представляют собой измерение в шкале отношений.

Шкала отношений допускает преобразования, изменяющие только масштаб, то есть преобразования подобия: F(Х) = аХ, где а > 0 (линейные возрастающие преобразования без свободного члена).
Примеры преобразования шкалы отношений:

• пересчёт цен из одной валюты в другую по фиксированному курсу;
• перевод массы из килограмм в фунты.

Базовая точка в шкале отношений одна — «единица». Эта условная «единица» может быть, например, 100 (проценты) или 1 (доли). Таким образом, измерения в долях и процентах эквивалентны, что очевидно и без всякой теории.
Однако выводы, которые делаются по результатам процентных измерений, могут быть ошибочными (см. врезку). Возникают сопутствующие вопросы:

• встречаются ли в практике управления подобные сравнения?
• какие проценты можно сравнивать друг с другом и для чего?
• какие действия с процентами можно производить?
• какие действия можно производить с индексами?

Корректность процентных измерений. Рейтинг путина vs стоимость свинины

•  Рейтинг путина: в январе 2014 — 60,6%, в июне 2014 — 87,4%.
•  Цена свинины: в январе — 116 руб/кг, в июне — 195 руб/кг.

Вывод: по темпам роста (в научной терминологии «прироста») свинина побеждает путина: 44% vs 68%.
Корректны ли эти измерения? Решите сами и объясните (что гораздо сложнее). Точно сформулировать, насколько такие сравнения корректны, удается лишь 10% слушателей программ МВА. Это ещё один довод в пользу изучения шкал. Хотя бы на уровне знакомства.

Шкала разностей допускает преобразование сдвига: F(Х) = Х + в. В такой шкале есть естественная единица измерения, но нет естественного начала отсчета. Базовая точка в шкале разностей тоже одна — условный „ноль”, своеобразная точка отсчёта. Пример: по шкале разностей измеряется время, если естественной единицей измерения принимаем год (или сутки — от полудня до полудня). На современном уровне знаний естественное начало отсчёта указать нельзя. Даже дату сотворения мира различные авторы рассчитывают по-разному, как и дату рождения Иисуса Христа.
Абсолютная шкала — это шкала, которая запрещает преобразования 5. Только для абсолютной шкалы результаты измерений (числа) используются в привычном смысле именно как числовые значения. В качестве примера измерений по абсолютной шкале можно привести число работников компании или выручку. При этом оценка выручки может отличаться от самой выручки (допустим, 20 млн руб. — „хорошо”, 24,5 млн руб. — „отлично”).
Кроме перечисленных шести основных типов количественных шкал, иногда используют и иные шкалы.

Степени свободы шкал

Для проведения измерений в шкалах отношений и разностей мы должны задавать одну точку. В шкале отношений она „играет роль единицы”, то есть соответствует переводу базового эмпирического элемента в единицу действительной оси. Для шкалы разностей это „нулевая точка”, то есть нужно задать отношение таким образом, чтобы „точка отсчёта” эмпирической системы превращалась в числовой ноль.
В этой связи математики различают шкалы по степеням свободы:

• 2 степени свободы имеют шкалы интервалов, степеней;
• 1 степень — шкалы отношений и разностей;
• 0 степеней — абсолютная шкала.

Иерархия шкал измерений

Напомним, что все шкалы делят на две большие группы: качественные и количественные. Наиболее распространённая классификация шкал — континуальная (рис. 3). В ней шкалы упорядочены по мере повышения их способности удовлетворять требованиям информативности и надёжности проведения оценок. Слева — самая слабая по информативности и самая надёжная, справа — наиболее информативная и наименее надёжная.

Рис. 3. Иерархия шкал измерений

https://tinyurl.com/mpt5zkym

Часть 1 - https://bit.ly/4ojmRoh

Управленческая теория измерений. Часть 1. О квалиметрии и теории измерений.

 

Андрей Мицкевич

Различные измерения и показатели используются в каждой фирме, в любой организации. Выбор подходов к оценке степени достижения некоторого показателя (например, плана продаж) огромен: тут сколько людей, фирм, ситуаций, видов работ, столько и мнений. Задача этой статьи — не придумывать что-либо своё, а попытаться классифицировать в самом общем виде доминирующее большинство существующих подходов к оценке степени достижения показателей.
Много ли вы слышали про научный подход к измерению показателей? А о науках о показателях? Практика использования показателей — это цельная картина или лоскутное одеяло? Если науки о показателях есть, то почему они не так широко распространены? Есть ли в них что-то полезное? Для ответа на эти вопросы представляю на суд читателей достижения науки в области измерения различных показателей.

Суха теория, мой друг,
Лишь древо жизни пышно зеленеет.
И. В. Гёте

Экономисты и менеджеры используют шкалы с незапамятных времен. Чаще всего шкалы и показатели используются для расчёта вознаграждения. Проблему шкалирования (влияния выбора шкал на выводы) изучали математики, а вот экономисты уделяли и уделяют мало внимания этой теме. Менеджеры практически не задумываются о том, какие шкалы и системы показателей они применяют для оценки результатов. Они редко корректно анализируют финансовые и управленческие последствия используемых шкал, не задумываются над математическими свойствами получаемой конструкции. А если и задумываются, то не слишком глубоко, ибо дел и без того хватает. Результат очевиден: получаемые системы показателей и системы управления, в которых они используются, никак не могут претендовать на почётное звание сбалансированных.

Менеджеры практически не задумываются о том, какие шкалы и системы показателей они применяют для оценки результатов. Результат — получаемые системы показателей и системы управления, в которых они используются, не могут претендовать на почётное звание сбалансированных.

Однако практика чаще всего бывает права, поскольку главное в сбалансированной системе показателей — это то, что если показатели, пусть и не очень хорошо шкалированные, стимулируют нужную активность, то этого зачастую бывает достаточно. Да и авторы BSC (Нортон и Каплан) тоже подтверждают это. Потому, наверное, теория показателей — управленческая теория измерений — не вышла на первые роли. Тем не менее, дело это важное. И начинать здесь надо с теории 1.

Современный этап интереса учёных к этой тематике начался в 1960-е годы. Термин «квалиметрия» был предложен в 1968 году группой советских научных работников (экономистов и инженеров) во главе с Азгальдовым Г. Г., выявивших методологическую общность способов количественного оценивания качества совершенно разных объектов. А в Австрии примерно в то же время Йозеф Пфанцагль создал теорию измерений.

Квалиметрия

Квалиметрия (в широком смысле) — это научная дисциплина, в рамках которой изучаются методология и проблематика комплексного количественного оценивания качества объектов любой природы [1]. Цель квалиметрии — получить комплексный, или интегральный, измеритель интересующего объекта или процесса.

Как и многие науки, квалиметрия претендует на всеобщность. Но основных полезных достижений квалиметрии немного. Объяснение этому лежит в том числе и в её широчайшем охвате, а как известно, «нельзя объять необъятное».

Достижение 1. Чёткое деление двух видов величин: измерений и оценок:

• измерение — первичный показатель, естественное, принятое в конкретной предметной области количественное отображение измеряемой величины;
• оценка — вторичный показатель.

Оценка в квалиметрии — это степень соответствия оцениваемых объектов тем правилам или закономерностям, по которым они теоретически должны формироваться в идеальном случае.

Все оценки должны основываться на эталоне.

Достижение 2. Виды оценок.

Оценки в квалиметрии могут быть двух видов:

• дифференциальными, или единичными, — относящимися к одному свойству;
• комплексными — оценивающими совокупность свойств.

Как правило, в качестве дифференциальных оценок показателей используют не абсолютные, а индексные показатели. Они меньше единицы и показывают, что степень достижения цели ещё далека от 100%. Хотя их значение может быть и больше единицы в случае превышения целевого значения.
В квалиметрии существует два вида индексных показателей, которые активно используются:

• индекс полезности типа Х, получаемый делением фактического значения показателя (Х) на его целевое значение (XG);
• индекс полезности типа Y получается делением целевого значения (YG) на фактическое значение показателя (Y).

Комплексная оценка помогает в целом охарактеризовать качество объекта или группу его свойств. Например, коэффициент готовности позволяет одновременно охарактеризовать и безотказность, и ремонтопригодность изделия:

Коэффициент готовности = Среднее время наработки на отказ / (Среднее время наработки на отказ + Среднее время восстановления)

Комплексные показатели бывают групповыми, интегральными и обобщёнными (рис. 1).

Рис. 1. Классификация показателей качества

Интегральный показатель (в квалиметрии) — это комплексный показатель, отражающий отношение суммарного полезного эффекта от использования объекта по назначению к затратам на создание и использование объекта по назначению. Например, для технического устройства часто используют такой интегральный показатель:

Интегральный показатель = Суммарный полезный эффект / (Затраты на создание + Затраты на эксплуатацию)

Надо отметить, что не всегда необходимость измерить суммарный полезный эффект вызывает проблемы. Например, для буровых установок суммарный полезный эффект может быть равен общей глубине проходки в метрах до капитального ремонта.
Обобщенный показатель — это показатель, относящийся к такой совокупности свойств объекта, по которой принято решение оценивать его качество в целом.

Функции полезности в квалиметрии Классическая комплексная оценка в квалиметрии основана на аддитивных функциях полезности. Аддитивные функции полезности доминируют в квалиметрии. Приведу выдержку из принципов квалиметрии [2]. При использовании метода комплексной оценки качества продукции все разноразмерные показатели свойств должны быть преобразованы и приведены к одной размерности или выражены в безразмерных единицах измерения. Кстати, в теории полезности это называется единообразным шкалированием [4]. При определении комплексного показателя качества каждый показатель отдельного свойства должен быть скорректирован коэффициентом его весомости. При количественной оценке качества, особенно по комплексному показателю, недопустимо использование взаимообусловленных и, следовательно, дублирующих показателей одного и того же свойства. Приведём формулы квалиметрии, которые используются в том числе и для того, чтобы

сравнить разные теории и подходы. Классическая комплексная оценка в квалиметрии — это U(x), где х — вектор частных измерений качества U, математически представляет собой аддитивную функцию полезности: где:  αi — веса оценок (показателей качества) задают относительную важность i-ого показателя в комплексном показателе качества и выполняются условия αi > 0 и αi = 1, можно представить комплексную оценку I и в процентах — тогда αi = 100;  xi — значение i-ого первичного показателя (в терминах квалиметрии это и есть измерение);  Ii(xi) — классическая квалиметрическая дифференциальная оценка i-ого показателя. Обратите внимание, что оценка основана на индексах (I), являющихся дифференциальными оценками частных показателей.

Достижение 3. Богатый опыт оценивания, выверенная междисциплинарная терминология.

Алгоритм комплексной оценки уровня качества в технической сфере показан на рис. 2.

Рис. 2. Алгоритм комплексной оценки уровня качества продукции

Теория измерений

Теория измерений пошла другим путём, чисто математическим. Математики выделяют три основные проблемы теории измерений [3].
1. Проблема представления: можно ли для некоторого объекта измерений 2 построить числовую систему, чтобы, оперируя числами, выразить всё, что необходимо для оценки, мотивации и принятия решений? 3 То есть можно ли построить шкалу, полностью описывающую объект для задач управления 4. Так, конечно, в идеале не бывает, хотя бы потому, что оцениваются объекты нечисловой природы. Но стремиться к этому надо.
Проблема представления связана с простым, но единственно важным для практики вопросом: влияет ли выбор шкал на выводы? Конечно, влияет. Например, в легкоатлетическом десятиборье чемпионами могут оказаться разные спортсмены, если использовать сегодняшнюю — довольно сложную — шкалу начисления очков или просто суммировать места по разным спортивным дисциплинам. Более того, последнее спровоцирует оппортунистическое поведение спортсменов. К примеру, если мой товарищ по команде лидирует после пяти видов соревнований и занимает 3-е место в метании диска, а его конкурент — на 7-м месте, можно помочь товарищу, „вклинившись” между ними. Это означает, что нарушено требование независимости измерений от состава и поведения участников.
По той же причине плохо ранжировать, например, конструкторов только на основе их квалификации. В этом случае необходимо строить шкалу, не зависящую от состава коллектива конструкторов. Наверняка она будет многокритериальной и довольно сложной. Но, по возможности, представительной и максимально отражающей представления людей о том, кто является сильнейшим десятиборцем или более квалифицированным инженером. Причём для выполнения разных задач могут быть выбраны разные конструкторы.
Можно ли сделать это с помощью чисел? Вот одна из задач теории измерений.
2. Проблема единственности: сколько вариантов числовой системы можно корректно использовать для описания эмпирической системы отношений? Её решение опирается на понятие допустимых преобразований.

Допустимые преобразования — это такие преобразования рассматриваемой шкалы измерений, которые не меняют соотношений между объектами измерения.

Практически всегда можно обосновать одну шкалу и вывести функцию её допустимых преобразований, тем самым определив массу шкал, удовлетворяющих заданным свойствам. Эта часть теории измерений нашла отражение в узком и не исчерпывающем практические нужды перечне типов шкал.

Важный для практики вопрос: влияет ли выбор шкал на выводы? Что за вопрос, конечно, влияет. Но мало кто об этом помнит, выбирая ту или иную шкалу.

3. Проблема адекватности или устойчивости шкалирования: можно ли делать адекватные выводы по результатам операций с числами шкал? Например, естественно требовать, чтобы выводы, сделанные на основании средних, зависели только от объекта управления, а не от выбранной шкалы.
Главные вопросы теории измерений. Прикладную суть теории измерений можно описать с помощью трёх вопросов, которые мы сформулируем, используя язык квалиметрии (это первая и самая естественная основа нашей теории управленческих измерений — обобщение и использование достижений предшественников). 5
Измерения.

•  Вопрос 1. К какой категории относятся измерения — к качественным или количественным? Измерить что-либо означает выразить числами. А стоит ли вообще это делать? Существуют ли «качественные измерения» или они обязательно должны быть «оцифрованными»?
•  Вопрос 2. Какие шкалы использовать? Если выбраны количественные измерения, какие ограничения накладываются на используемые числа? Эти ограничения как раз описываются типами шкал. Какие бывают шкалы и как ими правильно пользоваться, чтобы обеспечить достоверность выводов, сделанных на основе измерений?

Оценки.

•  Вопрос 3. Показатели используются для подведения итогов (оценок) на основе измерений. Какие арифметические действия при этом корректны? Как они связаны со шкалами? Какие выводы можно делать?

Коллизия (столкновение) теории и практики

Математики привыкли говорить логически строго, и практики не всегда точно их понимают. Потому полезность теории измерений на практике стремится к нулю — менеджеры её не знают (или не понимают, а потому игнорируют). Формально о шкалах можно прочесть в учебниках. Для математика этого достаточно, а для практика будет непонятно, «куда это засунуть», поэтому он использует не науку о шкалах, а своё представление о них. Получается как у классика: «Хотели как лучше…». Тем не менее, и практик чаще всего бывает прав, ибо главное в сбалансированной системе показателей (ССП) — что это «не проект из мер и весов». И даже если показатели не очень хорошо шкалированы, они могут стимулировать эффективную работу. Область учёных — те в целом не частые случаи, когда неграмотность порождает потери…

* * *

В следующей части статьи я попробую изложить теорию измерений популярно и полезно, не теряя, по возможности, математической строгости. Начну со шкал. При этом всю непривычную для менеджера математику — гомоморфизмы, изоморфизмы и прочее — оставим в стороне, а будем оперировать только минимумом упрощённых понятий и практическими выводами.

https://tinyurl.com/ytcmcvba